आईन्स्टाईन ला e=mc^2 हे ऐतिहासिक सूत्र कसं उलगडलं? “सापेक्षतावाद” नेमकं काय आहे? समजून घ्या

आमचे सर्व लेख मिळवण्यासाठी फॉलो करा : फेसबुक | ट्विटर | इंस्टाग्राम | टेलिग्राम । शेअरचॅट

–

व्हिडिओजसाठी फॉलो करा : इनमराठी युट्यूब चॅनल 

===

E=mc^2 हे equation Energy (ऊर्जा) आणि Mass (वस्तूमान) ह्यातील संबंध दाखवतं. ह्या जगप्रसिद्ध equation चा अर्थ आपल्याला माहित असतो. पण ते कसं derive केलं ते गणितं न घुसडता फक्त Idea यावी म्हणून हा लेख…

Theory of Relativity (सापेक्षतावादाचा सिद्धांत) हा frames of reference बद्दल आहे. आपल्याला माहित आहे कि, विश्वात कोणत्याही वस्तू (ग्रह, तारे , दीर्घिका) ह्या स्थिर नाहीत.

आता तुम्ही हा लेख वाचतांना जर स्थिर बसला असाल,  तरी ही पृथ्वी तुम्हाला घेऊन सेकंदाला ३० किलोमीटर वेगाने स्वतः भोवती फिरत आहे. तसेच पृथ्वी स्वतः भोवती फिरता फिरता सूर्याभोवती देखील फिरते आणि आपला सूर्य हा आ-काशगंगेच्या केंद्राभोवती फिरतो.

ह्या उदाहरणाने आपल्याला कल्पना येईल की, ह्या विश्वात कोणतीही गोष्ट स्थिर नाही. त्यामुळे प्रत्येकजन हे विश्व त्यांच्या त्यांच्या संदर्भ चौकटीतून (frames of referenceमधून) पाहत असतात. आणि सापेक्षतावादाचा सिद्धांत हा ह्याच विविध संदर्भ चौकटींमध्ये (frames of reference) दिसणाऱ्या निरीक्षणांमधील बदलांचा आढावा घेतो.

सापेक्षतावादाच्या सिद्धांतामागे दोन गृहीतके आहेत :

१. कोणत्याही संदर्भ चौकटीत (frame of reference मध्ये) भौतिकशास्त्राचे नियम समान आहेत.
हे गृहीतक जर सत्य मानले, तर प्रकाशाची गती (c=299,792,458 m/s म्हणजे साधारण सेकंदाला ३ लाख किलोमीटर एवढी आहे) जी विद्युतचुंबकत्वाच्या नियमांमुळे (laws of electromagnetism) आहे. (प्रकाश विद्युतचुंबकीय लहरींचा बनलेला असतो हे मॅक्सवेलने शोधले होते). म्हणून,

२. प्रकाशाची गती देखील प्रत्येक संदर्भ चौकटीत (c=299,792,458 m/s) समान असते.
हे देखील पहिल्या गृहीतकामुळे गृहीत धरावे लागते.

आईनस्टाईनच्या 1905 च्या विशेष सापेक्षता सिद्धांतानुसार (Special theory of Relativity) कोणतीही वस्तू (पदार्थ) ही प्रकाशाच्या वेगाहून जास्त गती गाठू शकत नाही . म्हणजेच प्रकाशाची गती ही वैश्विक वेग मर्यादा (cosmic speed limit) आहे. तसेच कोणत्याही frame of referenceमधून speed of light ही constantच दिसते हे देखील आपण गृहीत धरले. तसेच मायकलसन आणि मोर्ले ह्यांनी केलेल्या प्रयोगावरून ते सिद्ध ही झाले होते.

पण, जेव्हा कोणताही पदार्थ (matter) हा प्रकाशाच्या गतीच्या जेवढा जवळ जवळ जातो तेव्हा 3 गोष्टी नाट्यमयरित्या बदलतात (किंबहुना ती वेग मर्यादा गाठू न देण्यासाठी बदलतात) : Time (वेळ), Length (लांबी) , Mass (वस्तुमान).

1. Time Dilation : प्रकाशाच्या गतीच्या जेवढे जवळ जाऊ तेवढा ‘काळ’ आपल्यासाठी स्थिर जगापेक्षा मंदावतो.

 

 

ह्यासाठी जुळ्यांचा विरोधाभास (Twins paradox) खूप प्रसिद्ध आहे. जुळ्या भावांमधील एक भाऊ हा प्रकाशाच्या वेगाच्या जवळच्या गतीने अवकाशात प्रवास करून पृथ्वीवर परत येतो तेव्हा पृथ्वीवर थांबलेला भाऊ त्याच्या तुलनेने जास्त म्हातारा होतो. म्हणजे अवकाश सफरीवर गेलेल्या भावाचे वय (time) पृथ्वीवरच्या भावाच्या तुलनेत कमी वेगाने सरकते.

 

2. Length Contraction : प्रकाशाच्या गतीच्या जेवढे जवळ जाऊ तेवढी गतीच्या दिशेने असलेली आपली लांबी ही आकडते.

 

 

3. Increase in Mass : प्रकाशाच्या गतीच्या जेवढे जवळ जाऊ तेवढे आपले mass (वस्तूमान) वाढत जाते.

 

 

ही लक्षणे आपल्या रोजच्या आयुष्यात बघण्यात येत नाहीत. कारण, रोजच्या आयुष्यात आपण speed of lightच्या तुलनेने खूपच कमी (अगदी नगण्य) गतीने प्रवास करतो.

वरील point 1 आणि 2 मध्ये (वेळ आणि लांबीतील बदलांमूळे) आपण पाहू शकतो की, जेवढ्या जास्त गतीने आपण प्रवास करू तसे Time, Lengthच्या व्याख्या बदलतात. (but, velocity= distance/time) त्यामुळे सापेक्षावादानुसार दोन वेगवेगळ्या frame of reference मध्ये असलेल्या गतींची आपण सरळ सरळ बेरीज-वजाबाकी करू शकत नाही.

(जशी आपण आपल्या रोजच्या आयुष्यात करतो. For example – एका गाडीची गती 80 km/hr आहे आणि समोरून परंतु विरुद्ध दिशेने येणाऱ्या गाडीची गती देखील 80 km/hr आहे. तर त्यांची एकमेकांसाठी सापेक्षगती (relative speed) 80+80= 160 असेल. इथे सरळ बेरीज करून उत्तर मिळालं. पण पदार्थ जेव्हा प्रकाशाच्या गतीच्या जवळ प्रवास करत असतो तेव्हा अशी सरळ बेरीज करता येत नाही.)

तसेच इथे तिसरा point ही महत्वाचा ठरतो, तो म्हणजे Mass.

Mass हे Momentum (संवेग)ला direct affect करते.

न्यूटनच्या नियमानुसार, Momentum (संवेग) म्हणजे एखाद्या वस्तूच्या वस्तुमानाचा व वेगाचा गुणाकार असतो.

i.e. Momentum = Mass*velocity

Law of conservation of Momentum (संवेग अक्षय्यतेच्या नियमा) नुसार Momentum हा inertial frame of reference मध्ये constant राहतो.

(Inertial frame of reference म्हणजे जिथे acceleration नसतं . म्हणजेच velocity = constant.)

Law of conservation of Momentum (संवेग अक्षय्यतेच्या नियम) = जे आपण अकरावीत शिकलो, In case of elastic collision :

summation of momentums of two particles before collision = summation of momentums of particles after collision

M1V1+M2V2 = M1V1+M2V2

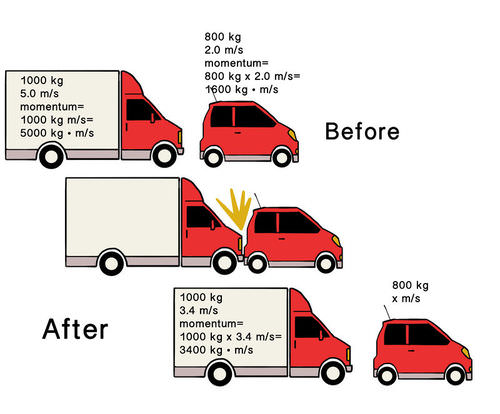
संवेग अक्षय्यतेचा नियम समझण्यासाठी हे उदाहरण मदत करू शकेल.

 

 

वेगवेगळे वस्तुमान आणि वेग असलेल्या दोन वाहनांची इथे टक्कर दाखवण्यात आली आहे. ही टक्कर जर आपण elastic (म्हणजे कुठल्याही वाहनांची टक्करीनंतर तोडफोड न होता) गृहीत धरू.

तसेच inelastic collisionमध्ये देखील संवेग अक्षय्यतेचा नियम पाळला जातो परंतु खोलात न शिरता इथे फक्त उदाहरणादाखल elastic collisionचे उदाहरण उचित ठरेल.

पण, इथे एक गोष्ट लक्षात घेण्यासारखी आहे की सापेक्षतावादानुसार गतीमुळे Mass (वस्तुमान) बदलतं आणि गतींची सरळ बेरीज वजाबाकी (direct addition/subtraction) पण करू शकत नाही.

म्हणून सापेक्षतावादाचे परिणाम लक्षात घेता न्यूटनने define केलेल्या Momentumच्या definitionनुसार (म्हणजे P=m.v), Law of conservation of Momentum पाळला जात नाही.

तो पाळला जाण्यासाठी (म्हणजे संवेग अक्षय्यतेचा नियम टिकवण्यासाठी) आपल्याला “Momentum” (संवेग) म्हणजे काय ह्याची सापेक्षतावादानुसार नवीन व्याख्या करावी लागते .

ही नवी व्याख्या ‘वेळे’ला चतुर्थमिती गृहीतधरून (Time as a 4th dimension लक्षात घेऊन) आईनस्टाईनने केली.

 

 

Minkowski Space-time : Considering ‘Time’ as a 4th Dimension. ह्या आकृतीत दाखवल्याप्रमाणे Horizontal axis हे अवकाशाच्या X,Y,Z ह्या तीन मिती दर्शवतात तर Vertical axis हा Time चा आहे.वरील Light Coneच्या आत जो भाग येतो ते आपले संभाव्य भविष्य (Possible Future) दाखवते. Speed of Lightची मर्यादा असल्यामुळे Light Coneच्या बाहेरचा भाग आपल्या संभाव्य भविष्यावर परिणाम (affect) करू शकत नाही.

वरील Light Cone जसा Futureसाठी आहे तसा खालील भाग हा Past Light Cone दाखवतो.

Time ला 0th dimension ,
X ला 1st,
Y ला 2nd,
Z ला 3rd.

 

 

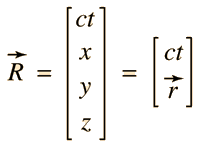
आईन्स्टाईनने spaceच्या ३ (X,Y,Z) आणि Time ची १ अशा ४ मिती (4 dimensions) गृहीत धरल्या. त्यातील space मधल्या dimensionsची एकके (units) ही लांबी (मीटर)ची आहेत तर वेळेचे एकक हे ‘सेकंद’ असते ते एकक हे लांबीत बदलण्यासाठी त्याला c (speed of light)शी गुणले. म्हणून आपण इथे ct,x,y,z अशी 4 dimensions घेतो.

असे 4 dimensions घेऊन 4-vector calculations करून असे दिसते, कि X,Y,Z ह्या spatial dimensionsचे components हे Kinetic Energy साठी आहेत (कारण गती ही ह्या spatial dimension XYZ चा function आहे)तर Time Dimensionचा component हा Rest Energy साठी असला पाहिजे.

गती अगदीच शून्य जरी धरली (considering all velocities along XYZ axes as Zero) तरी timeच्या dimensionचा component हा zero होत नाही. (बाकीचे X,Y,Z चे components zero होऊन जातात , पण timeचा component हा non-zeroच असतो.)

ह्याचा अर्थ ?

Particle स्थिर जरी असला (in rest) तरी त्याची energy non-zero असते त्याला ‘Rest Energy’ म्हणतात

हीच ती rest energy e = mc^2 …!

—

आमचं युट्यूब चॅनल आणि त्यावरचे व्हिडिओज बघण्यासाठी चॅनलला फॉलो करा :

–

===

व्हिडिओजसाठी फॉलो करा : इनमराठी युट्यूब चॅनल

–

 शेअरचॅटवर मिळवण्यासाठी क्लिक करा: इनमराठी शेअरचॅट ग्रुप

–

आता इनमराठीच्या लेखाच्या अपडेट्स मिळवा टेलिग्रामवर! जॉईन करा टेलिग्राम चॅनल: https://t.me/InMarathi

–

आमचे इतर लेख वाचण्यासाठी क्लिक करा: InMarathi.com | आमचे सर्व लेख मिळवण्यासाठी फॉलो करा : फेसबुक | ट्विटर | इंस्टाग्राम  | टेलिग्राम । शेअरचॅट | Copyright © InMarathi.com | All rights reserved.